
The actual voltage is 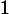
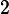





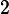



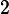
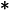
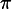
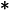
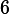
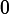
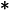

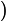 Volts. If we apply this voltage across a resistor of resistance
Volts. If we apply this voltage across a resistor of resistance 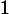

 the resistor will dissipate a time-varying power. What is the peak power (in Watts) dissipated by the resistor?
the resistor will dissipate a time-varying power. What is the peak power (in Watts) dissipated by the resistor?
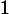
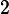
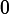
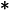





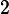
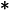

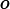


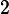
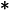
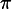
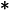
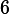
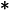

 Volts. If we apply this voltage across a resistor of resistance
Volts. If we apply this voltage across a resistor of resistance 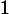
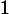

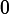
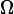 the resistor will dissipate a time-varying power. What is the peak power (in Watts) dissipated by the resistor?
the resistor will dissipate a time-varying power. What is the peak power (in Watts) dissipated by the resistor?
The voltage function has three terms; two constants and one that varies with time:
V(t) = 120 * sqrt(2) * cos(2 * π * 60 * t)
We know the cosine function takes on a maximum value of 1. So, the maximum value of the voltage function will be:
Vmax = 120 * sqrt(2) * 1 = 120 * sqrt(2)
So to find the peak power dissipated, we use the power equation P = IV.
Ppeak = I * Vmax
To find I, we need to use Ohm's Law to calculate the current through the resistor: V = IR
V = I * R
Vmax = I * R
Vmax / R = I
I = Vmax / R
So we substitute that back into our peak power equation:
Ppeak = (Vmax / R) * Vmax
Ppeak = Vmax*Vmax / R
Ppeak = 120*120*sqrt(2)*sqrt(2) / 110.0
Ppeak = 261.8 V
What is the average power (in Watts) dissipated by the resistor? (Hint: you compute the average power by integrating the power over one cycle of the waveform.)
Someone by the forum name of no47 posted the complete math to solve this problem on the forums:
The answer obtained is: 1440/11 Watts = ~131W
Instead we look down at the last paragraph of the answers and see a statement about time-varying voltage, constant voltage, and RMS voltage. So, we skip down to the third question on constant voltage and come back to this one...
... okay, good, you're back. The answer down there was ~131W and agrees with the answer that no47 provided on the forums, so that's a good sign. So let's check out this RMS concept; how can we calculate the RMS voltage from the peak voltage?
Wikipedia has the answers in the Root mean square (RMS) article:
By taking the square root of both these equations and multiplying them together, we get the equation
but since the interval is a whole number of complete cycles (per definition of RMS), the  terms will cancel out, leaving:
terms will cancel out, leaving:
 terms will cancel out, leaving:
terms will cancel out, leaving:
A similar analysis leads to the analogous equation for sinusoidal voltage:
Where 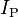 represents the peak current and
represents the peak current and 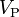 represents the peak voltage. It bears repeating that these two solutions are for a sinusoidal wave only.
represents the peak voltage. It bears repeating that these two solutions are for a sinusoidal wave only.
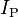 represents the peak current and
represents the peak current and 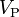 represents the peak voltage. It bears repeating that these two solutions are for a sinusoidal wave only.
represents the peak voltage. It bears repeating that these two solutions are for a sinusoidal wave only.
Pavg = Irms * Vrms
Pavg = Vrms*Vrms / R
Vrms = Vmax / sqrt(2) = (120 * sqrt(2)) / sqrt(2) = 120
Pavg = (120*120) / 110 = 14400 / 110 = 1440 / 11
Pavg = 1440 / 11 Watts = ~131 Watts
What would be the power (in Watts) dissipated by the resistor if the voltage was a constant value of 120V?
We use the power equation to calculate this: P = IV
P = I * V
But we also need the current, so we use Ohm's Law (V = IR) to calculate the current:
V = I * R
V / R = I
I = V / R
So we substitute that back into our power equation:
P = (V / R) * V
P = (V*V) / R
P = (120 * 120) / 110
P = 14400 / 110 = 1440 / 11 = ~131 W
If a time-varying voltage dissipates the same power in a resistor as a constant voltage would dissipate, we say that the time-varying voltage has the RMS value of the constant. RMS is an abbreviation for Root-Mean-Square.
Good to know.

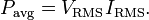
![I_{\mathrm{RMS}} = I_\mathrm{p}\sqrt {{1 \over {T_2-T_1}} \left [ {{t \over 2}} \right ]_{T_1}^{T_2} } = I_\mathrm{p}\sqrt {{1 \over {T_2-T_1}} {{{T_2-T_1} \over 2}} } = {I_\mathrm{p} \over {\sqrt 2}}.](http://upload.wikimedia.org/wikipedia/en/math/0/8/5/08543cd57af0274c61f600bc7803acf3.png)
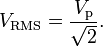
Thank you so much for this!
ReplyDelete"Someone by the forum name of no47"
ReplyDeletewhere is this forum?