S1E8: KCL

In the circuit shown there are six unknown elements.

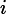
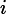
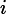
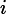
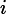
By measurements we have values for three of the branch currents: , , and .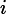

[Note: The courseware wants the expression on the right-hand side of the equals; leave off the "i4 =" on the left hand side, and be careful of the case of i vs. I]

Again, we need to pick two conventions:

• The sign of the term given the direction of the current arrow
• The direction for tracing the branches

To make things simple, we'll follow the same convention as last time:

• We'll trace the branch from the far node toward the chosen node.
• Traversing a current arrow from tail to head will be a positive term in the equation
• Traversing a current arrow from head to tail will be a negative term in the equation

In terms of the known currents, write an algebraic expression for the current ?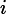 

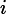
i4 is connected to two nodes, and the one on the right (middle of the circuit) has two other knowns, so that makes it a good candidate for the node.

(+i4) + (-i2) + (+i3) = 0

And now we solve in terms of i4:

i4 = i2 - i3

Write an algebraic expression for the current ?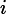

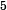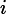
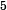i5 is also connected to two nodes. Because we just solved for i4, the node on the left otherwise has a known and a solved current, making it a good candidate.

(-i1) + (-i4) + (-i5) = 0

And now we solve in terms of i5:

(-i5) = i1 + i4

i5 = (-i1) + (-i4)

And we substitute for i4:

i5 = (-i1) + (-(i2 - i3))

i5 = (-i1) + (i3 + (-i2))

i5 = i3 - i2 - i1

Write an algebraic expression for the current ?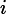

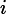
i6 is also connected to two nodes. The one on the left has two known currents, making it a good candidate for the choice of node.

i1 + i2 + i6 = 0

And now we solve in terms of i6:

i6 = -i1 - i2