In the circuit shown:

the strength of the source is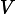


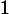
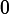 V, and the resistance of the resistor is
V, and the resistance of the resistor is 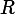

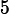
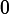
 .
.
The power dissipated in the resistor is given by the equation: P = IV

the strength of the source is
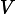


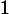
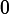 V, and the resistance of the resistor is
V, and the resistance of the resistor is 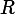

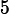
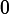
 .
. The power dissipated in the resistor is given by the equation: P = IV
P = I * 10
What is I?
To discover I, we need to use Ohm's Law to calculate the current flowing through the resistor:
V = IR
V / R = I
I = V / R
I = 10 / 50 = 1 / 5 = 0.2A
P = 0.2 * 10 = 2 Watts
What is the power dissipated in the resistor (in Watts)? 2
To balance the 2 Watts leaving the source, we consider -2 W to be entering the source. Therefore the source has no net change in charge over time (per our Lumped Element Abstraction assumptions).
What is the power entering the source (in Watts)? -2
No comments:
Post a Comment