
The strength of the source 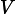 is given. Also, there are two known branch voltages: we know
is given. Also, there are two known branch voltages: we know 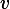
 and
and 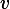
 .
.
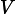 is given. Also, there are two known branch voltages: we know
is given. Also, there are two known branch voltages: we know 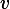
 and
and 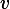
 .
. We will follow our convention:
- When we cross from - to +, this is a "positive" term in our equation.
- When we cross from + to - this is a "negative" term in our equation.
Remember that we can pick either direction (clockwise or counter-clockwise), and we can pick any loop (small or large) so long as we end up in the same spot.
In terms of the known voltages, write an algebraic expression for the branch voltage 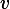
 :
:
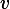
 :
:Since V and v1 are known, we'll use the left-most loop of this circuit. Starting in the lower left-hand corner and going clockwise:
(+V) + (-v1) + (-v3) = 0
(-v3) = (-V) + (+v1)
v3 = V - v1
[Note: The courseware wants "V - v1" as the answer; leave out the "v3 =", and watch the case on the V.]
Write an algebraic expression for the branch voltage 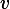
 :
:
Since V and v2 are known, we'll use the outer-most loop of the entire circuit. Starting in the lower left-hand corner and going clockwise:
(+V) + (+v4) + (-v2) = 0
v4 = v2 - V
[Note: The courseware wants "v2 - V" as the answer; leave out the "v4 =", and watch the case on the V.]
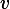
 :
:Since V and v2 are known, we'll use the outer-most loop of the entire circuit. Starting in the lower left-hand corner and going clockwise:
(+V) + (+v4) + (-v2) = 0
v4 = v2 - V
[Note: The courseware wants "v2 - V" as the answer; leave out the "v4 =", and watch the case on the V.]
Write an algebraic expression for the branch voltage 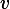
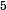 :
:
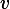
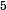 :
:This one is a bit more tricky, because v5 is only a part of two loops that also contain another unknown. So, we'll need to substitute one of the expressions that we already worked out. Let's take the top loop, starting at the node above v3 and proceeding clockwise:
(+v1) + (+v4) + (-v5) = 0
(-v5) = (-v1) + (-v4)
v5 = v1 + v4
And now we substitute our expression for v4:
v5 = v1 + v2 - V
[Note: The courseware wants "v1 + v2 - V" as the answer; leave out the "v5 =", and watch the case on the V.]
No comments:
Post a Comment