S1E2: Power

The picture shows a resistor connected to some unknown network N. The resistor is immersed in an isolated water bath, and its temperature is observed and recorded. The resistor has resistance .

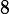
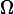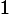
By observing the rate of increase of the temperature in the water bath, it is determined that the power dissipated in the resistor is W. 

So this is similar to S1E1.5 except that we are calculating it from the opposite direction. The power dissipated in the resistor is given by the equation P = IV

11 = I * V

We are looking for the answer in terms of V, so we need to solve Ohm's Law in terms of I.

V = IR

V / R = I

I = V / R

So we substitute that back into our equation power equation:

11 = (V / R) * V

V*V / R = 11

Now we put in the given value of the resistor:

V*V / 8 = 11

And solve for V:

V*V = 88

V = sqrt(88)

V = 9.4 Volts

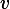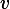Assuming that the voltage across the resistor is constant, what is the voltage (in Volts) across the resistor?
v: 9.4

The voltage is constant (9.4 V) and this is a simple linear resistor (8 Ohms), so Ohm's Law will tell us the current:

V = IR

V / R = I

I = 9.4 / 8

I = 1.2 A

But, look very carefully at the circuit diagram! The current arrow is pointing from the positive terminal into the network. This is the opposite direction that we usually consider current to flow, so we have to change the sign.

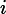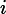What is the current (in Amperes) entering the network N from the resistor? 

i: -1.2