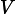

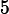

 V and
V and 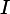

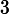

 , and that the resistors have the resistances
, and that the resistors have the resistances 


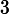


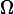 and
and 


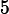


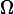 .
.
There are three node potentials labeled in this network 
 ,
, 
 , and
, and 
 . We can choose any node to be the reference node (the ground) from which voltages are measured, setting the corresponding node potential to zero. (Only voltages, which are differences of node potentials, are physically meaningful.) Let's start by choosing the ground at the negative terminal of the voltage source, so
. We can choose any node to be the reference node (the ground) from which voltages are measured, setting the corresponding node potential to zero. (Only voltages, which are differences of node potentials, are physically meaningful.) Let's start by choosing the ground at the negative terminal of the voltage source, so 


 .
.

 ,
, 
 , and
, and 
 . We can choose any node to be the reference node (the ground) from which voltages are measured, setting the corresponding node potential to zero. (Only voltages, which are differences of node potentials, are physically meaningful.) Let's start by choosing the ground at the negative terminal of the voltage source, so
. We can choose any node to be the reference node (the ground) from which voltages are measured, setting the corresponding node potential to zero. (Only voltages, which are differences of node potentials, are physically meaningful.) Let's start by choosing the ground at the negative terminal of the voltage source, so 


 .
.
Ok. e3 = 0 Volts
What is the value (in Volts) of the node potential

 ?
?5.0
Now there is one remaining unknown node, with potential

 . Write a node equation for that node.
. Write a node equation for that node.(e2-e1)g1 + (e2)g2 - I = 0
What is the value (in Volts) of 
 ?
?

 ?
?
(e2-e1)g1 + (e2)g2 - I = 0
(e2-e1)g1 + (e2)g2 = I
e2g1 - e1g1 + e2g2 = I
(e2-e1)g1 + (e2)g2 = I
e2g1 - e1g1 + e2g2 = I
e2g1 + e2g2 = I + e1g1
e2 (g1 + g2) = I + e1g1
e2 = I + e1g1 / (g1 + g2)
e2 = (3.0 + 5.0/3.0) / (1/3.0 + 1/5.0) = 4.67 / 0.53 = 8.81
e2 (g1 + g2) = I + e1g1
e2 = I + e1g1 / (g1 + g2)
e2 = (3.0 + 5.0/3.0) / (1/3.0 + 1/5.0) = 4.67 / 0.53 = 8.81
What is the voltage (in Volts) 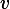
 across the resistor with resistance
across the resistor with resistance 
 ?
?
The voltage difference between e2 (8.81) and e3 (0) is 8.81; therefore the voltage across the resistor is 8.81.
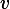
 across the resistor with resistance
across the resistor with resistance 
 ?
?The voltage difference between e2 (8.81) and e3 (0) is 8.81; therefore the voltage across the resistor is 8.81.
Now, let's start again. Suppose we chose a different node as the ground reference. Let's choose the top terminal of the current source, where it connects to the two resistors. So now 


 , and there are two remaining nodes. But if we know
, and there are two remaining nodes. But if we know 
 then we know that
then we know that 




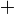
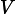 , so we still have only one unknown. What is the value (in Volts) of the node potential
, so we still have only one unknown. What is the value (in Volts) of the node potential 
 ?
?
e2' = e2 - 8.81
e3' = e3 - 8.81
e3' = -8.81



 , and there are two remaining nodes. But if we know
, and there are two remaining nodes. But if we know 
 then we know that
then we know that 




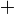
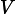 , so we still have only one unknown. What is the value (in Volts) of the node potential
, so we still have only one unknown. What is the value (in Volts) of the node potential 
 ?
?e2' = e2 - 8.81
e3' = e3 - 8.81
e3' = -8.81
Now, what is the voltage (in volts) 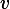
 across the resistor with resistance
across the resistor with resistance 
 ?
?
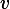
 across the resistor with resistance
across the resistor with resistance 
 ?
?8.81
Notice that the voltage across the resistor is the same, independent of the choice of the node chosen for the reference potential. Indeed, the physics does not care about the potentials, only the voltages that are their differences.
No comments:
Post a Comment