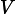

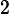

 V,
V, 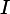

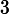

 A,
A, 





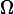 , and
, and 


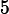


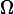 .
.
Wow, this one was a little tricky. I went to the forums and found an answer by UXO:
Short answer: apply KVL to the left-hand loop:
-V + i1R1 + i2R2 = 0
Then use your observation that i2 = i1 + I
=> -V + i1R1 + i1R2 + I*R2 = 0
i1 (R1 + R2) = V - I*R2
i1 = (V-(I R2))/(R1 + R2) = (2-3*5)/(4+5) = -1.44
Then just plug values back in and determine the rest of the unknowns.
So to recap, we KVL the left-hand loop:
-V + (i1*R1) + (i2*R2) = 0
Then we do a KCL on the node above R2:
-i1 + i2 - I = 0
Now we solve the KCL equation in terms of i2:
i2 = i1 + I
Then we substitute that into the KVL equation:
-V + (i1*R1) + ((i1 + I)*R2) = 0
Now we distribute R2 over the replaced i2:
-V + (i1*R1) + (i1*R2) + (I*R2) = 0
Then we solve this equation in terms of i1:
(i1*R1) + (i1*R2) + (I*R2) = V
(i1*R1) + (i1*R2) = V - (I * R2)
i1 * (R1 + R2) = V - (I * R2)
i1 = (V - (I * R2)) / (R1 + R2)
And then we plug in the values:
i1 = (2.0 - (3.0 * 5.0)) / (4.0 + 5.0) = (2.0 - (15.0)) / (9.0) = -13.0 / 9.0 = -1.44 Amps
With that in hand, we can determine the other currents:
-i1 + i2 - I = 0
i2 = I + i1
i2 = 3.0 - 1.44 = 1.56 Amps
And with those in hand, we can determine the voltages:
v1 = i1 * R1
v1 = -1.44 * 4.0 = -5.76 Volts
v2 = i2 * R2
v2 = 1.56 * 5.0 = 7.8 Volts
What is the voltage (in Volts) 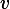
 across the resistor with resistance
across the resistor with resistance 
 ?
?
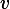
 across the resistor with resistance
across the resistor with resistance 
 ?
?
7.8
What is the power (in Watts) dissipated by the resistor with resistance 
 ?
?

 ?
?
P = IV
P = i2 * v2
P = 1.56 * -5.76 = 12.2 Watts
What is the current (in Amperes) 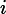
 through the resistor with resistance
through the resistor with resistance 
 ?
?
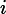
 through the resistor with resistance
through the resistor with resistance 
 ?
?
-1.44
What is the power (in Watts) dissipated by the resistor with resistance 
 ?
?

 ?
?
P = IV
P = i1 * v1
P = -1.44 * -5.76 = 8.3 Watts
What is the power (in Watts) supplied by the voltage source?
P = IV
P = -1.44 * 2.0 = -2.88 Watts
What is the power (in Watts) supplied by the current source?
P1 + P2 = Pr1 + Pr2
P2 = Pr1 + Pr2 - P1
P2 = 8.3 + 12.2 - (-2.88) = 23.4 Watts
You should observe that the sum of the power supplied by the sources is the sum of the power dissipated by the resistors. If this is not true you have done something wrong.
Thanks, had trouble with this one.
ReplyDeleteThanks and that i have a dandy provide: Who Repairs House Windows Near Me house renos before and after
ReplyDelete