
It is suggested in section 1.5.1 of the textbook that to increase the current-capacity of a battery without increasing the voltage at the terminals we can connect batteries of the same voltage in parallel. Let's examine this using our model.

Let's assume that both component batteries have the same voltage 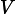


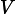


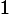

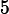 . The internal resistances of small batteries are about
. The internal resistances of small batteries are about 

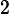
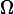 , but they vary a bit. Let's assume that
, but they vary a bit. Let's assume that 




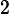
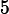 and
and 




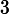
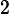 . What is the open-circuit voltage (in Volts)
. What is the open-circuit voltage (in Volts) 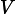 of the combination?
of the combination?
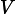


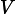


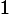

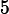 . The internal resistances of small batteries are about
. The internal resistances of small batteries are about 

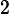
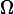 , but they vary a bit. Let's assume that
, but they vary a bit. Let's assume that 




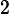
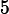 and
and 




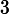
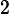 . What is the open-circuit voltage (in Volts)
. What is the open-circuit voltage (in Volts) 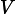 of the combination?
of the combination?
The voltages V1 and V2 are defined as 1.5; the only thing that might affect it would be a voltage drop across the resistors R1 and R2. So let's go to Ohm's Law: V= IR
Vdrop = I * R
Since the open circuit has zero current flowing through it, I = 0
Vdrop = 0 * R = 0 V
Thus the open-circuit voltage must be 1.5 V.
Now, suppose we short-circuit the compound battery. (This is very dangerous. NEVER do this to a large battery, such as a lead-acid battery in a car, or to a lithium-ion battery from your laptop. You MAY live to regret it, but you may not.) What is the current (in Amperes) you should expect to go through the short circuit?
We're looking for the current going through the short circuit. We'll use KCL to discover the currents entering the node above R2. (Ohm's Law in terms of current is: I = V/R)
i1 = V1 / R1
i2 = V2 / R2
i3 = ?
(+i1) + (+i2) + (-i3) = 0
(-i3) = (-i1) + (-i2)
i3 = i1 + i2
i3 = (V1 / R1) + (V2 / R2)
i3 = (1.5 / 0.25) + (1.5 / 0.32) = 6 + 4.7 = 10.7 A
We can think of this combination as a bigger battery of the same voltage as the two component batteries. What is the equivalent resistance (in Ohms) of the compound battery? (Hint: you have the voltage with nothing connected and the current when shorted out.)
Let's use Ohm's Law in terms of resistance to figure it out: R = V / I
R = 1.5 / 10.7 = 0.14 Ohms
Now, suppose that the voltages of the two component batteries are not quite the same. For example, suppose that 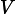


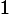

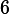 . Then when we hook the two batteries together current will flow and the higher voltage battery will charge the lower voltage one. What is the current (in Amperes) that will flow?
. Then when we hook the two batteries together current will flow and the higher voltage battery will charge the lower voltage one. What is the current (in Amperes) that will flow?
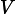


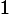

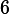 . Then when we hook the two batteries together current will flow and the higher voltage battery will charge the lower voltage one. What is the current (in Amperes) that will flow?
. Then when we hook the two batteries together current will flow and the higher voltage battery will charge the lower voltage one. What is the current (in Amperes) that will flow?
We choose the node above R2 and formulate a KCL equation:
The current (i2) on the branch that includes V2 and R2 will be pointing at our chosen node.
The current (i1) on the branch that includes V1 and R1 will be pointing away from our chosen node.
So by our convention, the equation is:
(+i2) + (-i1) = 0
i2 = i1
This shows there will be one current. That current will be given by Ohm's Law: I = V / R
So the question is .. what is V and what is R?
V will be the difference between the two votages: 1.6 - 1.5 = 0.1 Volts
R will be the sum of the resistors: 0.25 + 0.32 = 0.57 Ohm
I = 0.1 / 0.57 = 0.18 A
The current (i2) on the branch that includes V2 and R2 will be pointing at our chosen node.
The current (i1) on the branch that includes V1 and R1 will be pointing away from our chosen node.
So by our convention, the equation is:
(+i2) + (-i1) = 0
i2 = i1
This shows there will be one current. That current will be given by Ohm's Law: I = V / R
So the question is .. what is V and what is R?
V will be the difference between the two votages: 1.6 - 1.5 = 0.1 Volts
R will be the sum of the resistors: 0.25 + 0.32 = 0.57 Ohm
I = 0.1 / 0.57 = 0.18 A
Thanks, for such a great post. I have tried and found it really helpful. For more details to visit ev technician training
ReplyDelete